存储树型结构
下文主要想和大家分享,在DB中存储和查询树的4种方式,第4种方式存疑;
引言
那么理想中的树型结构应具备哪些特点呢?
- 数据存储冗余小、直观性强;
- 方便返回整个树型结构数据,也可以很轻松的返回某一子树(方便分层加载);
- 快速获以某节点的祖谱路径;
- 插入、删除、移动节点效率高等等;
父ID + 递归算法
使用递归算法。category 表中一个字段id,一个字段 fid(父id)。这样可以根据 WHERE id = fid 来判断上一级内容,运用递归至最顶层。
优点:
- 数据库结构设计简单,程序上实现容易;
- 增删改分类很轻松;
- 用频率最多的,大部分开源程序也是这么处理,不过一般都只用到四级分类;
缺点
- 分类组装数据时,读取不太方便,如果分类到更多级,那是不可取的办法;
注:这种方案有很多变种,可以通过加额外的字段如层数或者缓存存储,一定程度上提高效率;
父ID集合字段
设置 fid 字段类型为 varchar,将父类id都集中在这个字段里,用符号隔开,比如:1,3,6。这样更容易得到各上级分类的ID。
查询某个分类下所有分类的时候可以使用:
1 | SELECT * FROM category WHERE pid LIKE "1,3%" |
优点:
- 相比于递归算法,在读取数据方面优势非常大;
- 数据库结构设计简单;
缺点:
- 若查找该分类的所有 父分类 或者 子分类 查询的效率也不是很高,至少也要二次query;
- 在增删改分类非常麻烦;
- 倘若递增到无限级,还需考虑存储字段是否达到要求;
注: 自我感觉,这算是一种奇淫技巧,可维护性差
闭包表(ClosureTable)
原理
ClosureTable 本质上是存储所有的路径信息,进而表明节点之间的关系;
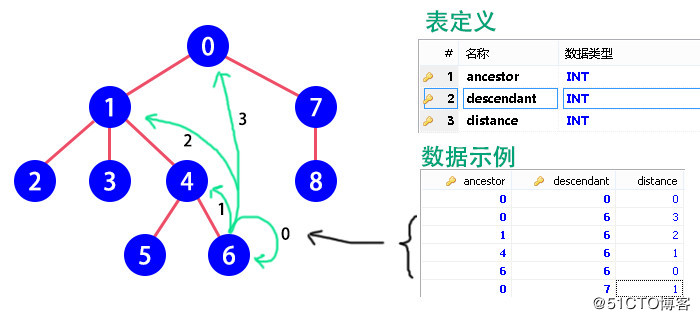
定义关系表CategoryTree,其包含3个字段:
- ancestor 祖先:上级节点的id
- descendant 子代:下级节点的id
- distance 距离:子代到祖先中间隔了几级
原理:这三个字段的组合是唯一的,因为在树中一条路径可以标识一个节点,所以可以直接把它们的组合作为主键。
如何处理查询操作
- 子节点查询
查询 id 为5的节点的子节点:
1 | SELECT descendant FROM CategoryTree WHERE ancestor=5 AND distance=1 |
查询 id 为5的节点的子孙节点:
1 | SELECT descendant FROM CategoryTree WHERE ancestor=5 AND distance>0 |
- 路径查询
查询由根节点到 id 为10的节点之间的所有节点,按照层级由小到大排序
1 | SELECT ancestor FROM CategoryTree WHERE descendant=10 ORDER BY distance DESC |
查询 id 为10的节点(含)到id为3的节点(不含)之间的所有节点,按照层级由小到大排序
1 | SELECT ancestor FROM CategoryTree WHERE descendant = 10 AND distance < ( SELECT distance FROM CategoryTree WHERE descendant = 10 AND ancestor = 3) ORDER BY distance DESC |
注:查询路径,只需要知道 descendant 即可,因为 descendant 字段所在的行就是记录这个节点与其上级节点的关系。如果要过滤掉一些则可以限制 distance 的值。
- 查询节点所在的层级(深度)
查询id为5的节点是第几级的
1 | SELECT distance FROM CategoryTree WHERE descendant=5 AND ancestor=0 |
查询id为5的节点是id为10的节点往下第几级
1 | SELECT distance FROM CategoryTree WHERE descendant=5 AND ancestor=10 |
注:查询层级(深度)非常简单,因为distance字段就代表层级;直接以上下级的节点id为条件,查询距离即可。
- 查询某一层的所有节点
查询所有第三层的节点
1 | SELECT descendant FROM CategoryTree WHERE ancestor=0 AND distance=3 |
问题2:怎样进行插入、删除和移动操作
插入: 当一个节点插入到某个父节点下方时,它将具有与父节点相似的路径,然后再加上一个自身连接即可。
因此,插入操作需要两条语句,第一条复制父节点的所有记录,并把这些记录的distance加一,因为子节点到每个上级节点的距离都比它的父节点多一。当然descendant也要改成自己的。
例如:把id为10的节点插入到id为5的节点下方
1
2
3
4
5
6
7
8
9
10INSERT INTO CategoryTree(ancestor , descendant , distance)(
SELECT
ancestor ,
10 ,
distance + 1
FROM
CategoryTree
WHERE
descendant = 5
)然后就是加入自身连接的记录。
1
INSERT INTO CategoryTree(ancestor,descendant,distance) VALUES(10,10,0)
删除:
1
DELETE FROM CategoryTree WHERE descendant=5
移动: 因为新位置所在的深度、路径都可能不一样,这就导致移动操作不是仅靠UPDATE语句能完成的,因此选择删除+插入实现移动。
如果存在子树,上级节点的移动还将导致下级节点的路径改变,所以移动上级节点之后还需要修复下级节点的记录,这就需要递归所有下级节点。
优点
对于树结构常用的查询都能够很方便的处理。
缺点
插入和移动就不是很方便
参考资料
https://www.percona.com/blog/2011/02/14/moving-subtrees-in-closure-table/
https://technobytz.com/closure_table_store_hierarchical_data.html
前序遍历树模型(The Nested Set Model)
来自网络博文 https://www.cnblogs.com/wllyy189/archive/2009/08/17/1547877.html ,自觉插入逻辑上有问题,当是扩展的一个思路吧
原理解释
先把树按照水平方式摆开,从根节点“Food”开始,然后它的左边写上1。然后按照树的顺序(从上到下)给“Fruit”的左边写上2。这样,你沿着树的边界走啊走(这就是“遍历”),然后同时在每个节点的左边和右边写上数字。最后,我们回到了根节点“Food”在右边写上18;
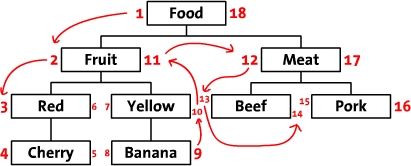
左右值暗示了每个节点之间的关系。例如:“Red”有3和6两个值,所以,它是有拥有1-18值的“Food”节点的后续。同样的,我们可以推断所有左值大于2并且右值小于11的节点,都是有2-11的“Fruit” 节点的后续。因此,树的结构就通过左值和右值储存下来了。这种数遍整棵树算节点的方法叫做“改进前序遍历树”算法。
表结构设计:
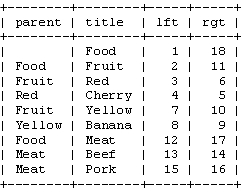
查询操作
如何通过一个SQL语句把所有的分类都查询出来呢,而且要求如果是子类的话前面要打几个空格以表现是子分类?
查询所有分类很好办
1 | SELECT * FROM category WHERE lft>1 AND lft<18 ORDER BY lft |
但如何区分谁是谁的子类呢?
观察发现,如果相邻的两条记录,第一条的右值比第二条右值大那么就是他的父类,比如:Food 的右值是18而 Fruit 的右值是11 那么food是fruit的父类,但是又要考虑到多级目录。
于是有了下面的设计:用一个数组来存储上一条记录的右值,再把它和本条记录的右值比较,如果前者比后者小,说明不是父子关系,就弹出数组,否则就保留,之后根据数组的大小来打印空格,这样就解决了这个问题。
更新操作
如何进行插入、删除和移动操作?
插入:插入操作很简单找到其父节点,之后把左值和右值大于父节点左值的节点的左右值加上2,之后再插入本节点,左右值分别为父节点左值加一和加二,可以用一个事务来操作:
删除:
- 得到要删除节点的左右值,并得到他们的差再加一,@mywidth = @rgt - @lft + 1;
- 删除左右值在本节点之间的节点 3.修改条件为大于本节点右值的所有节点,操作为把他们的左右值都减去
移动: 暂时没发现什么规律,只好先删除再插入
特点
- 查询方便,但是增删改操作有点繁琐,适合更新操作不是很多,查询多的场景